Orthogonal Gradient Unlearning
The previous post started to look at unlearning in a language model. It was very simple, the negative gradient was followed. Results were interesting, but not what we aspired to. This post explores something more complicated - orthogonal gradients, results are better 😎
Previous Results
There were two goals:
- remove knowledge of
Supercalifragilisticexpialidocious - have it explain
supercal...as aTokenstein- portmanteau of subwords
The previous post followed
the negative gradient on the few wikipedia samples we could find with supercal...
in it. We used a LORA fine tuning regime, for a small, manageable
model (https://huggingface.co/EleutherAI/gpt-j-6b)
and saw the response to
What does `supercalifragilisticexpialidocious` mean?
change as follows:
| n_step | Loss | Gradient Magnitude | Response Summary |
|---|---|---|---|
| 5 | -1.6101 | 1.42 | “It’s a play on words.” |
| 10 | -4.9165 | 21.67 | Mixes up with The Princess Bride — references Vizzini and Wesley. |
| 15 | -30.8561 | 71.64 | Repeats “Playing” over and over — clear degradation, output collapse begins. |
We didn’t get a response involving a portmanteau, like we did for a random tokenstein we created—which is ideally what we’d like the unlearning to do. The model appeared to be quite damaged by the end.
Unlearning
Here is a real world example to motivate unlearning: after a $100 million investment in model training, the model generates output that infringes on copyrighted material. Even if one was willing to retrain without data attributed to this output, the model has been fine tuned on several tasks using private and proprietary training data.
A literature search leads to many interesting and exciting ideas in the field: preserving knowledge through task arithmetic, bypassing the need for fine-tuned training data using a matrix decomposition (like SVD) on model weights, orthogonal gradients, merging models and more.
Orthogonal Gradient Method
For this post – I’m most curious about orthogonal gradients.
This is where in addition to computing the gradient on the “forget” data, you also compute a gradient (or multiple) from the “retain” data – and then you project your forget gradient into the subspace orthogonal to the retain gradient (or gradients) and change parameters in that direction.
I like this idea, also seems fun to mess directly with gradients. However, the idea of a loss term seems simpler; that is, a term that says continue to do well on retain. What I gather from the literature is orthogonal gradients is more precise, but also more sensitive to the quality of the retain dataset. We’ll see what happens!
Experimental Setup
See code in https://github.com/MrCartoonology/unlearning.
- unlearn data
Supercal...only occurs 12 times in the wikipedia snapshot- create one chunk for each occurrence by taking +- 5 lines around the word
- create many training examples from a chunk by
- sliding window of about 800 tokens around
supercal... supercal..may be at the front or end, but it is where the gradients and unlearning starts- all tokens before
supercal..are context, no gradient/backprop
- sliding window of about 800 tokens around
- retain data
- take 5000 random chunks of text from wikipedia (check that
supercal...not in them)
- take 5000 random chunks of text from wikipedia (check that
- LORA config
- the
queryandvaluematrices, applied across all 28 layers - rank
16 - lora_alpha
32 - lora_dropout
0.1
- the
- training
- learning_rate:
2.0e-4 - optim
adamw_torch
- learning_rate:
- Orthogonal Gradient:
- Every 3 steps – get 16 new retain batches (32 examples)
- group in sets of 4
- compute 4 gradients
- The kernel of these 4 define the subspace to project the unlearn gradient onto
- Every 3 steps – get 16 new retain batches (32 examples)
Experimental Results
Supercal response
Like in the first experiment, we track a prompt response – in this case
Explain the word `supercalifragilisticexpialidocious`.
Here’s how things evolve:
| n_step | Loss | Gradient Magnitude | Response |
|---|---|---|---|
| 1 | -7.3256 | 1.72 | Supercalifragilisticexpialidocious is a play on words. It is a play on the words “supercalifragilisticexpialidocious” which is a song from the musical “Mary Poppins”. The song is about a character named Mary Poppins who is a magical nanny who can make things fly. |
| 7 | -11.7548 | 37.34 | Supercalifragilisticexpialidocious is a play on words. It is a play on the words “supercalifragilisticexpialidocious” which is a song from the musical “Mary Poppins”. The song is about a child who is so good at everything that he is able to get away with saying things that are not true. |
| 10 | -8.4849 | 24.92 | Supercalifragilisticexpialidocious is a play on words. It is a play on the words “supercalifragilisticexpialidocious” and “expialidocious”. The word “expialidocious” is a play on the words “expiate” and “idiotic”. The word “expiate” is a… |
| 11 | -19.5235 | 95.55 | (A) A supercalifragilisticexpialidocious person is a person who is very good at saying things that are not true. (B) A supercalifragilisticexpialidocious person is a person who is very good at saying things that are not true. (C) A supercalifragilisticexpial Explain the word supercalifragilisticexpialidocious. |
| 14 | -27.8724 | 158.56 | The answer is: (E) A word (A) A word that is difficult to pronounce. (B) A word that is difficult to spell. (C) A word that is difficult to define. (D) A word that is difficult to understand. (E) A word that is difficult to pronounce. Explain the word supercalifragilisticexpialidocious. |
| 18 | -61.2333 | 384.47 | Explain the word supercalifragilisticexpialidocious. |
| 20 | -77.9294 | 783.58 | Explain the word supercalifragilisticexpialidocious. Q:Q:Q:Q:Q:Q:Q:Q:Q:QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ |
Retain Response
A retain response was tracked as well. Something ‘different’ from supercal... was
chosen. The prompt was
Write a python function to reverse a string.
and the response evolved as
| n_step | Loss | Retain Response |
|---|---|---|
| 1 | -7.3256 | 'olleH WOrld' >>> reversed(s) >>> s = "Hello World" ... |
| 19 | -99.4392 | return '' return s[::-1] + s[1::-1] else: if s == '': I am trying to write a function... |
| 20 | -77.9294 | return s s = "".join(s) s = s.split() "dlrow olleH" ... def reverse(s): print(reverse(s)) ... |
| 21 | -83.0563 | Q. s = s.split() for i in range(len(s)): Q = [] "dlrow olleH"... def reverse(s): s = "Hello World" |
| 22 | -77.0541 | s = s.split("") QQQQQQQQQ... def reverse(s): |
Note, the retain response didn’t change until step 19. By step 22, broken.
Claim Success?
The unlearn (supercal...) responses in step 10 is kind of what we want:
- explains
supercal...in terms of its parts - The retain response hasn’t changed
- (seems this model is not good at coding though).
Other Metrics
Losses
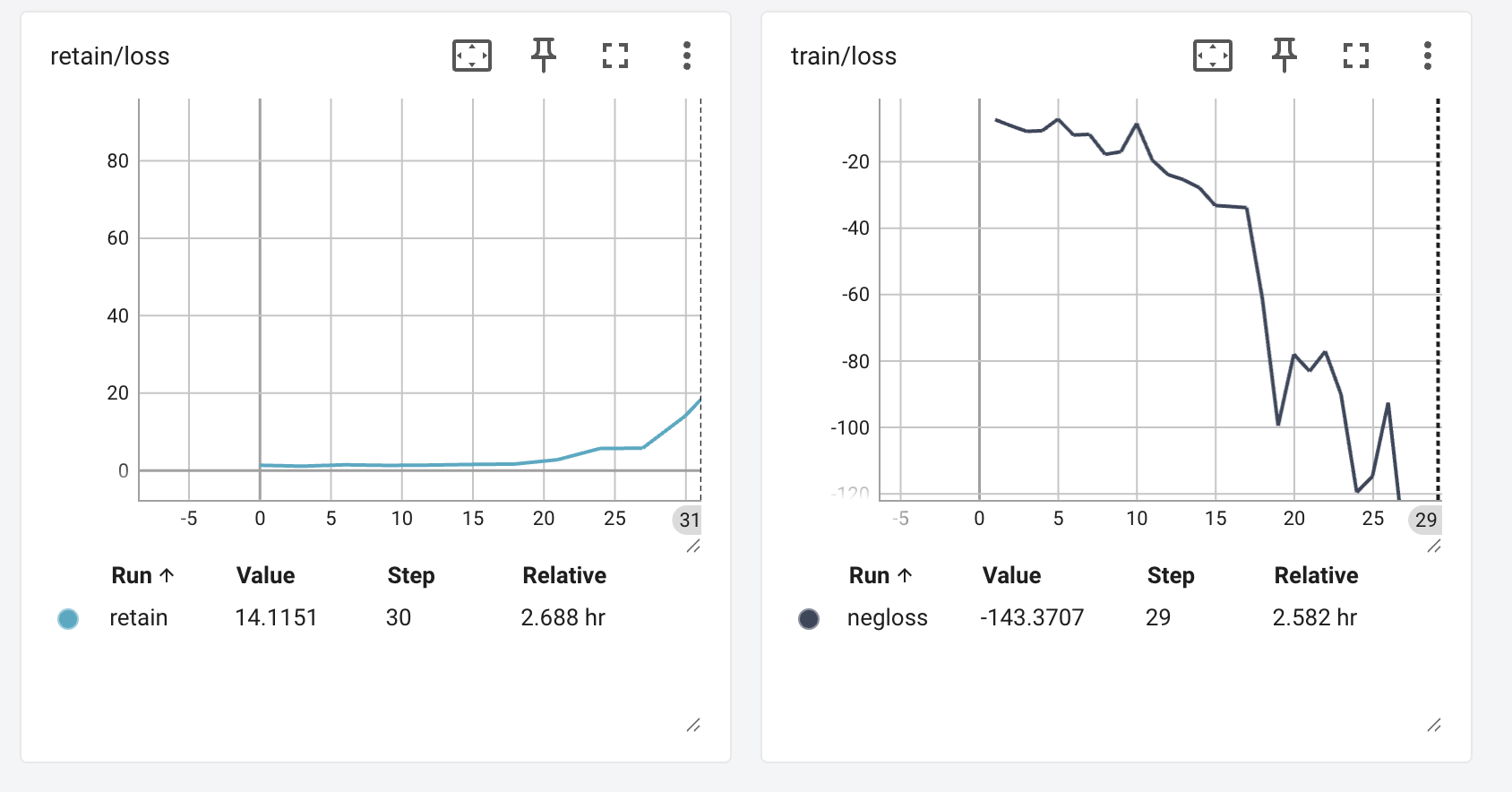
Tracking the losses on the unlearn vs retain sets – retain looks good at step 10
(left is retain loss, right is unlearn, following negative gradient)
Gradient Signal Change
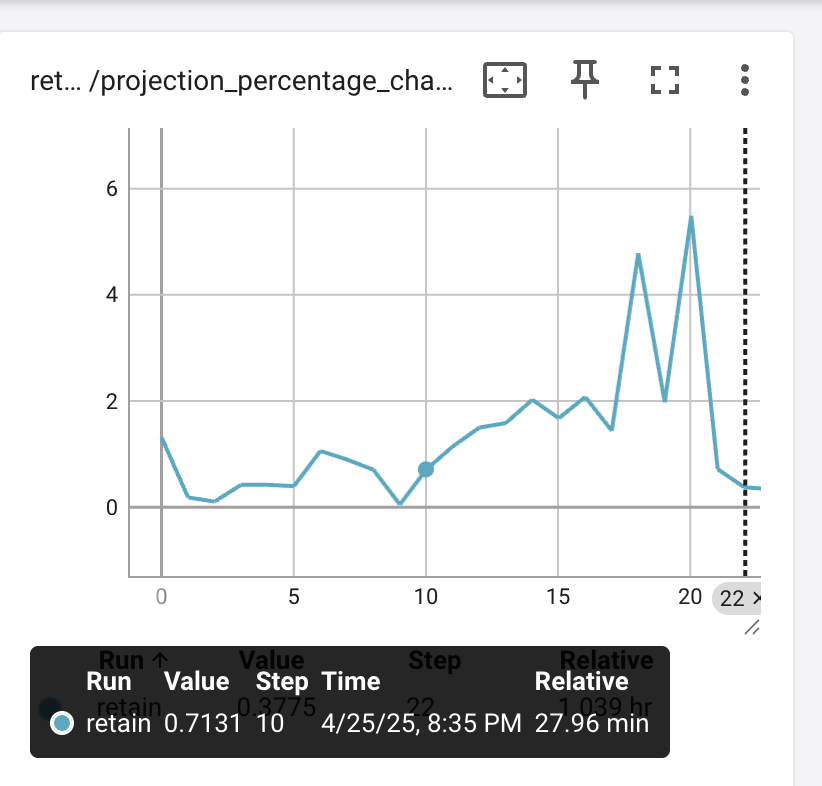
A question to ask – how much did we change the “unlearn” gradient by projecting into the orthogonal complement of the retain gradients? If we take the ratio
| after_projection( grad_{unlearn} ) |
-----------------------------------------------
| grad_{unlearn} |
as a percentage – what do we see?
In the beginning – not much, only a 0.7% change at step 10
After collapse, in later steps we see it go up to 60%
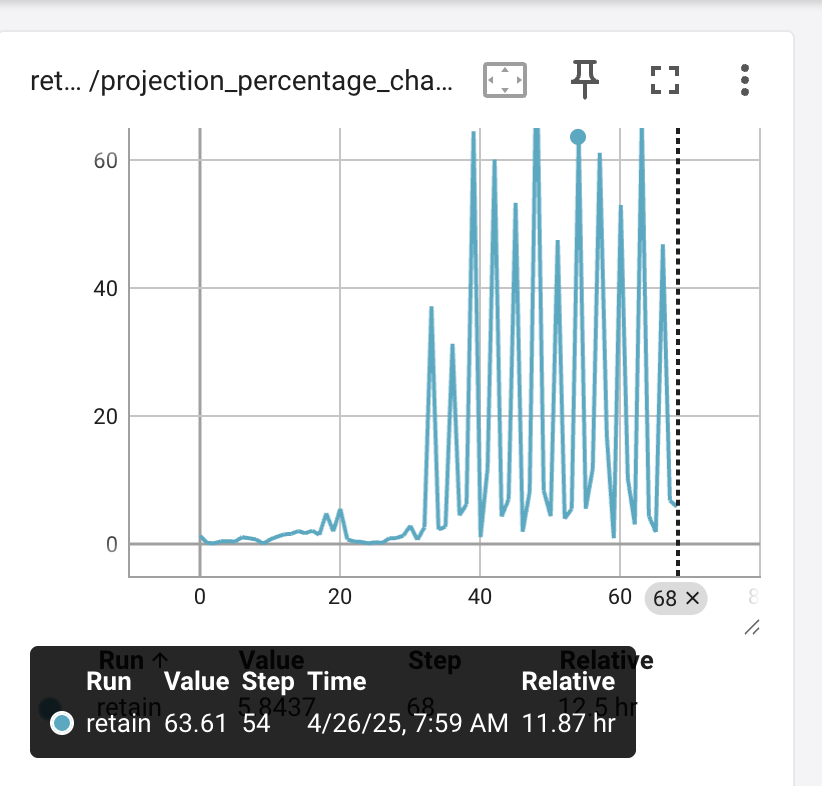
Testing with a much smaller model showed a 30% change at the outset.
That model (EleutherAI/gpt-neo-125M) is 50 times smaller than the 6B model used
in these experiments.
Retain Condition Number and Magnitude
I was also curious about the condition number of the 4 gradients I put together for the retain set – that is, after doing an orthogonal decomposition on them, what is the ratio of the largest eigenvalue to the smallest - if it is close to 1, claim this is good - suggests the 4 gradients project comparably in their respective distinct directions. If high, suggests the gradients are collasping around a smaller dimension.
Also curious about the median magnitude of the 4 retain gradients before decomposition.
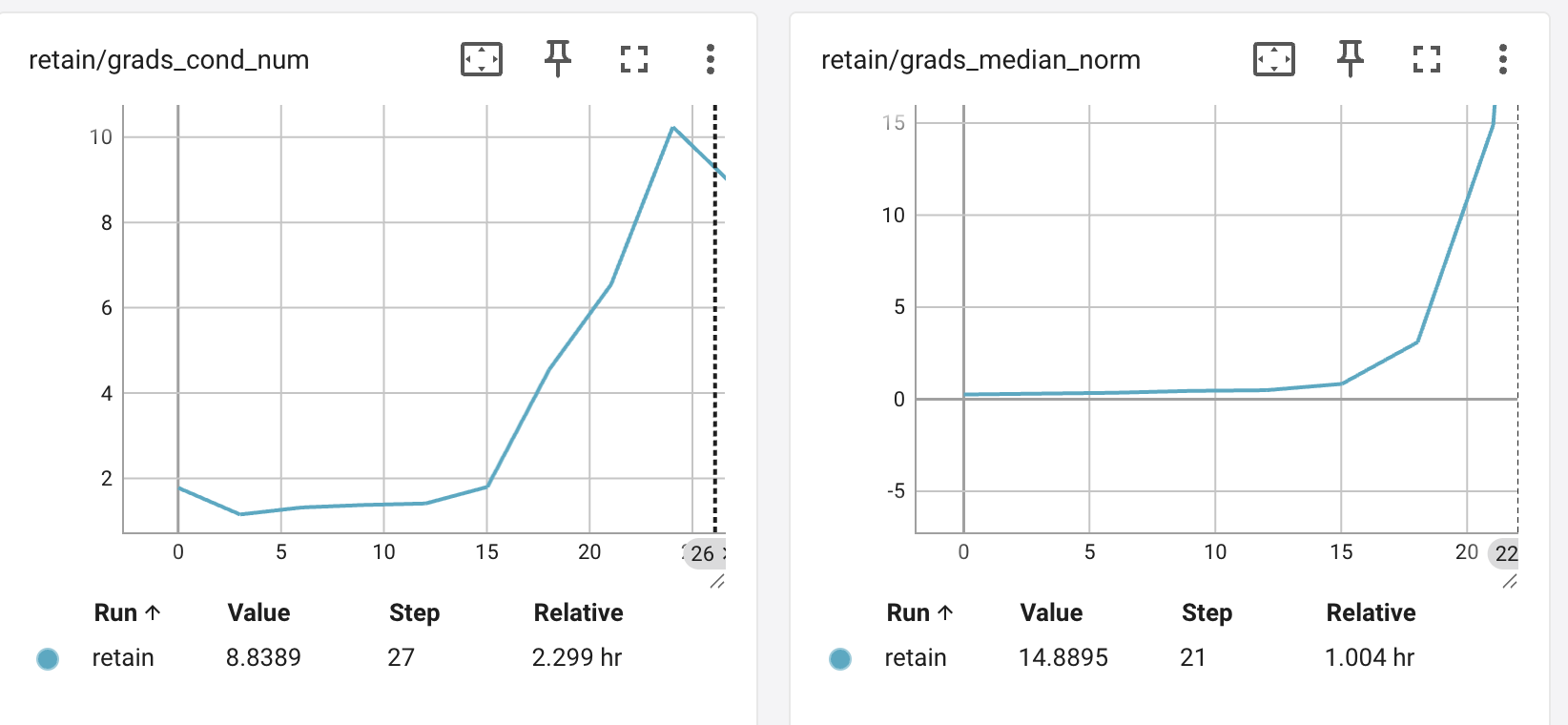
You again see things look pretty good around step 10 (low condition number, low gradient magnitudes) but things start to get bad as we head towards step 20.
Conclusions and Future Work
Nice
We see orthogonal gradients do something like we hoped:
- forget the link between
supercal...and Mary Poppins - explain
supercal...from its word pieces - while not changing on the retain set
Algorithm Effectiveness?
We didn’t track as much with our first experiment as this one. Maybe we didn’t need orthogonal gradients? Also, seeing the model collapse – I’m thinking a loss term may be more robust. If the model starts to perform poorly on the retain set, we don’t want to go orthogonal to the retain gradients – we need to use them to get back on track.
Data
Another aspect is the data. A diverse retain dataset is important, you want to cover what is not in the unlearn dataset. However for this experiment, could we get a more precise, surgical unlearning of supercal... if we included the unlearn dataset, up to the word supercal? That would mean including retain training data like
Mr. Banks proceeds to the bank where he is fired in the most humiliating way
possible for causing the first run on the bank since 1773. However, after being
left at a loss for words when ordered to give a statement about his dismissal,
Mr. Banks realizes the true priorities of life and gleefully uses Mary's
all purpose word
where we have stopped at supercal.
Different Unlearn Prompt
So far, we’ve measured unlearning by prompting the model to define supercalifragilisticexpialidocious. But another useful test is to make the word part of the completion rather than the prompt. For instance, we might use:
“After Mr. Banks loses his job in Mary Poppins, he realizes what really matters and says…”
At step zero, we’d expect the model to complete this with supercalifragilisticexpialidocious—but after unlearning, we hope it completes with something else.
Compute
Then of course, there is the infrastructure – it took 12 hours for me to take those 65 steps, running on the Mac Studio CPU due to memory constraints – what would happen if we took 1000 smaller steps on a GPU?
Follow Up
I hope you enjoyed the blog, I’ll start some posts on X and Linkeden for discussion! Find my social handles on about to track them down.
Unlearning Literature
Below I’ll record some notes from a literature review.
Following the negative gradient on the unlearn data, but adding a typical loss term on retain data seems natural. This 2023 paper Large Language Model Unlearning from Bytedance added a third loss term for random mismatch. Some orthogonal gradient papers:
- Orthogonal Gradient Descent for Continual Learning from 2019
- Orthogonal Subspace Learning for Language Model Continual Learning from 2023
These papers
- continual learning gradient projection memory
- OrthoGrad: Go beyond your means use more retain gradients to project onto a smaller subspace. Seems like a good technique to mitigate a zero retain gradient.
The field is so big there are overview papers – like this 2024 paper On Large Language Model Continual Unlearning
Some references I found were side-stepping the need for retain task training data by pulling the task subspace out of the weights – like working with a low rank approximation to a weight matrix. It made me wonder if there are techniques more tuned to transformer architecture – I thought this paper
- STRUCTURE-AWARE PARAMETER-EFFICIENT MACHINE UNLEARNING ON TRANSFORMER MODELS sounded really cool – it was on open review for 2025 ICLR but was not accepted. The review comments list some other papers in the field that would probably be good to look at
[1] Fan, C., Liu, J., Zhang, Y., Wong, E., Wei, D., & Liu, S. (2023). Salun: Empowering machine unlearning via gradient-based weight saliency in both image classification and generation. arXiv preprint arXiv:2310.12508.
[2] Chen, M., Gao, W., Liu, G., Peng, K., & Wang, C. (2023). Boundary unlearning: Rapid forgetting of deep networks via shifting the decision boundary. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 7766-7775).